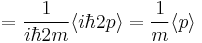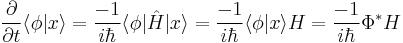Ehrenfest theorem
| Quantum mechanics |
|---|
 |
| Introduction Glossary · History |
|
Background
|
|
Fundamental concepts
Complementarity · Decoherence
Duality · Ehrenfest theorem Entanglement · Exclusion Measurement · Probability amplitude Nonlocality · Quantum state Superposition · Tunnelling Uncertainty · Wave function |
|
Formulations
|
|
Equations
|
|
Advanced topics
|
|
Scientists
Bell · Bohm · Bohr · Born · Bose
de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner |
The Ehrenfest theorem, named after Paul Ehrenfest, the Austrian physicist and mathematician, relates the time derivative of the expectation value for a quantum mechanical operator to the commutator of that operator with the Hamiltonian of the system. It is
where A is some QM operator and 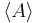 is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg picture of quantum mechanics, where it is just the expectation value of the Heisenberg equation of motion.
is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg picture of quantum mechanics, where it is just the expectation value of the Heisenberg equation of motion.
Ehrenfest's theorem is closely related to Liouville's theorem from Hamiltonian mechanics, which involves the Poisson bracket instead of a commutator. In fact, it is a rule of thumb that a theorem in quantum mechanics which contains a commutator can be turned into a theorem in classical mechanics by changing the commutator into a Poisson bracket and multiplying by 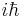 . This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.
. This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.
Derivation
Suppose some system is presently in a quantum state 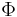 . If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition
. If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition
where we are integrating over all space. If we apply the Schrödinger equation, we find that
and
Notice 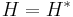 because the Hamiltonian is hermitian. Placing this into the above equation we have
because the Hamiltonian is hermitian. Placing this into the above equation we have
Often (but not always) the operator A is time independent, so that its derivative is zero and we can ignore the last term.
General example
For the very general example of a massive particle moving in a potential, the Hamiltonian is simply
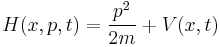
where  is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum
is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum  . Using Ehrenfest's theorem, we have
. Using Ehrenfest's theorem, we have
since the operator  commutes with itself and has no time dependence.[2] By expanding the right-hand-side, replacing p by
commutes with itself and has no time dependence.[2] By expanding the right-hand-side, replacing p by 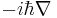 , we get
, we get
After applying the product rule on the second term, we have
but we recognize this as Newton's second law. This is an example of the correspondence principle, the result manifests as Newton's second law in the case of having so many particles that the net motion is given exactly by the expectation value of a single particle.
Similarly we can obtain the instantaneous change in the position expectation value.
This result is again in accord with the classical equation.
Notes
- ^ In bra-ket notation
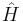 is the Hamiltonian operator, and H is the Hamiltonian represented in coordinate space (as is the case in the derivation above). In other words, we applied the adjoint operation to the entire Schrödinger equation, which flipped the order of operations for H and
is the Hamiltonian operator, and H is the Hamiltonian represented in coordinate space (as is the case in the derivation above). In other words, we applied the adjoint operation to the entire Schrödinger equation, which flipped the order of operations for H and 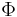 .
. - ^ Although the expectation value of the momentum
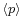 , which is a real-number-valued function of time, will have time dependence, the momentum operator
, which is a real-number-valued function of time, will have time dependence, the momentum operator 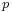 does not. Rather, the momentum operator is a constant linear operator on the Hilbert space of the system. The time dependence of the expectation value is due to the time evolution of the wavefunction for which the expectation value is calculated. An Ad hoc example of an operator which does have time dependence is
does not. Rather, the momentum operator is a constant linear operator on the Hilbert space of the system. The time dependence of the expectation value is due to the time evolution of the wavefunction for which the expectation value is calculated. An Ad hoc example of an operator which does have time dependence is 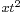 , where
, where 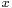 is the ordinary position operator and
is the ordinary position operator and 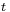 is just the (non-operator) time.
is just the (non-operator) time.
![\frac{d}{dt}\langle A\rangle = \frac{1}{i\hbar}\langle [A,H] \rangle%2B \left\langle \frac{\partial A}{\partial t}\right\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/522045c7de6b34559bfe2f35fdd25f8e.png)
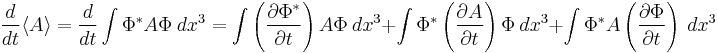
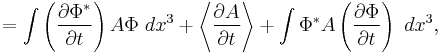
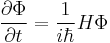
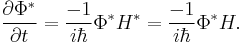
![\frac{d}{dt}\langle A\rangle = \frac{1}{i\hbar}\int \Phi^* (AH-HA) \Phi~dx^3 %2B \left\langle \frac{\partial A}{\partial t}\right\rangle = \frac{1}{i\hbar}\langle [A,H]\rangle %2B \left\langle \frac{\partial A}{\partial t}\right\rangle.](/2012-wikipedia_en_all_nopic_01_2012/I/b9cdbc2b9d1ebdefc9df0d4efdc7b855.png)
![\frac{d}{dt}\langle p\rangle = \frac{1}{i\hbar}\langle [p,H]\rangle %2B \left\langle \frac{\partial p}{\partial t}\right\rangle = \frac{1}{i\hbar}\langle [p,V(x,t)]\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/48cafaf06a0440585aa82c78d30b7e72.png)
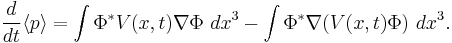
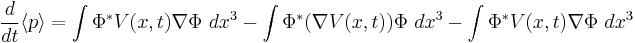
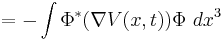
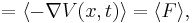
![\frac{d}{dt}\langle x\rangle = \frac{1}{i\hbar}\langle [x,H]\rangle %2B \left\langle \frac{\partial x}{\partial t}\right\rangle =](/2012-wikipedia_en_all_nopic_01_2012/I/cde30dbc07366d778ac2fd6cc455f88b.png)
![= \frac{1}{i\hbar}\langle [x,\frac{p^2}{2m} %2B V(x,t)]\rangle %2B 0 = \frac{1}{i\hbar}\langle [x,\frac{p^2}{2m}]\rangle =](/2012-wikipedia_en_all_nopic_01_2012/I/501b41d8d76dd5e90cf9124837dd3bc8.png)
![= \frac{1}{i\hbar}\langle [x,\frac{p^2}{2m} %2B V(x,t)]\rangle = \frac{1}{i\hbar 2 m}\langle [x,p] \frac{d}{dp} p^2\rangle =](/2012-wikipedia_en_all_nopic_01_2012/I/69fac4757c887dd600f608c63045edec.png)